In 2015, I worked to implement the so-called "compact" Hilbert index. You can read about it here. After some feedback on the code, I decided that I wanted to investigate "how good" the compact Hilbert actually is. In this post, I compare my code to Chris Hamilton's original code (using a program by Peter Colberg) and verify the basic promise of the compact Hilbert index (keep the ordering of the full Hilbert index).

What is already out there

I am aware of the following softwares for computing the compact Hilbert index:

1. Chris Hamilton published libhilbert. His academic webpage has been removed but I had a copy of the library. I provide a copy of his "0.2.1" version on my GitHub account. The code is LGPL v2.1 so it can be redistributed.
2. Peter Colberg has an implementation in his simulation software nano-dimer. This is what motivated me to use the compact Hilbert index in the first place. Peter Colberg has a test against Chris Hamilton's implementation. This code is MIT and implemented in OpenCL C.
3. I have implemented the code in Python for my own understanding here and in Fortran for my simulation code RMPCDMD.

Are jumps "allowed" in the compact Hilbert curve?

By construction of the orginal Hilbert curve, consecutive points along the curve are at a distance of 1 from each other.

One question that came several times (I can still count on one hand though) is about the existence of jumps in the curve. The only promise in the compact Hilbert index paper is that it preserves the ordering of the Hilbert curve HR08. By graphical observations, some non-cubic curves can be seen as "repeat" of the cubic curve. But this simple situation does not hold for arbitrary shapes.

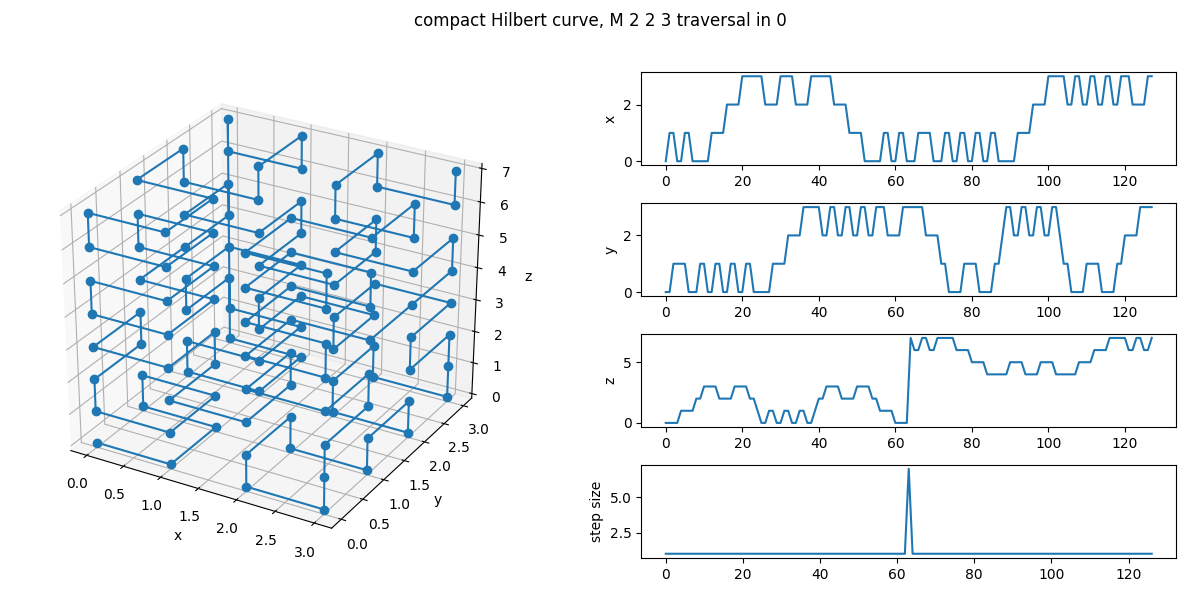
For "M = [2 2 3]", I show below an example where the dimension of first traversal of the curve is 0. One can see that around the middle of the curve, there is a jump in the z direction that is larger than one. This is reflected in the step size of the lower-right panel.

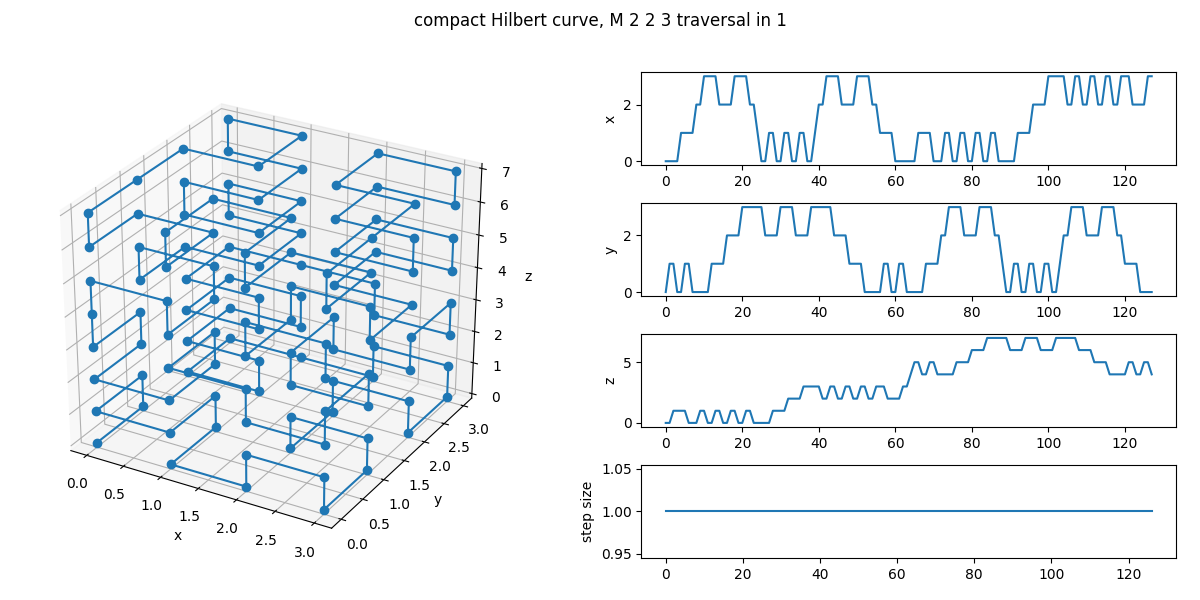
In the next illustration, I have only changed the parameter vd to 1 and now there is no jump anymore.

Actual testing

To perform the testing, I compiled the library by Chris Hamilton and used Peter Colberg's hilbert test program that will dump the coordinates of a hilbert curve in a HDF5 file.

Then, I dumped my code for the Hilbert curve in a Python file. The code relies on knowing the spatial dimension (in the code it is N) first and was not super suited to write a proper library. The dimensions of the curve are given as a set of integers ("2 2 3" in the example above) and there is the option --vd to specify the dimension of first traversal.

A plain cubic Hilbert curve is generated and the relative ordering of the compact indices with respect to the original one is performed (with success, ouf) at every run of the program. So this settles the fulfillment of the ordering.

When the option --compare is given, the program will load the data generated by the hilbert program and compare it against the Python data. So far, all combinations of dimensions did work.

The test program is called test_compact_hilbert.py and is available in the repository that I set up specifically for these tests. To display a compact hilbert curve, simply ask, for instance

python3 test_compact_hilbert.py 1 2 3 --plot --vd 2

To perform preset tests with the code, simply issue the command

make HDF5_HOME=/path/to/hdf5lib

(The variable HDF5_HOME is only necessary on the first invocation when the program hilbert is built.)

Summary

To gain confidence in my code, I have

1. Made a backup of the original code by the author of the algorithm. That was just in time, as its homepage disappeared.
2. Made a specific Python test program to test my algorithm against the reference one.
3. Checked numerically the ordering of the curve.
4. Adapted my program to also allow an easy graphical inspection of the compact Hilbert curve and pass as an argument the direction of traversal.

Bibliography

• HR08 Chris H. Hamilton and Andrew Rau-Chaplin. Compact Hilbert indices: Space-filling curves for domains with unequal side lengths, Information Processing Letters 105, 155-163 (2008).