2.5.3. Linear System Solvers

• sparse matrix/eigenvalue problem solvers live in scipy.sparse.linalg

• the submodules:

  • dsolve: direct factorization methods for solving linear systems
  • isolve: iterative methods for solving linear systems
  • eigen: sparse eigenvalue problem solvers

• all solvers are accessible from:

  >>> import scipy.sparse.linalg as spla
  >>> spla.__all__    
  ['LinearOperator', 'Tester', 'arpack', 'aslinearoperator', 'bicg',
  'bicgstab', 'cg', 'cgs', 'csc_matrix', 'csr_matrix', 'dsolve',
  'eigen', 'eigen_symmetric', 'factorized', 'gmres', 'interface',
  'isolve', 'iterative', 'lgmres', 'linsolve', 'lobpcg', 'lsqr',
  'minres', 'np', 'qmr', 'speigs', 'spilu', 'splu', 'spsolve', 'svd',
  'test', 'umfpack', 'use_solver', 'utils', 'warnings']
  

2.5.3.1. Sparse Direct Solvers

• default solver: SuperLU 4.0

  • included in SciPy
  • real and complex systems
  • both single and double precision

• optional: umfpack

  • real and complex systems
  • double precision only
  • recommended for performance
  • wrappers now live in scikits.umfpack
  • check-out the new scikits.suitesparse by Nathaniel Smith

Examples

• import the whole module, and see its docstring:

  >>> from scipy.sparse.linalg import dsolve
  >>> help(dsolve) 
  

• both superlu and umfpack can be used (if the latter is installed) as follows:

  • prepare a linear system:

    >>> import numpy as np
    >>> from scipy import sparse
    >>> mtx = sparse.spdiags([[1, 2, 3, 4, 5], [6, 5, 8, 9, 10]], [0, 1], 5, 5)
    >>> mtx.todense()
    matrix([[ 1,  5,  0,  0,  0],
            [ 0,  2,  8,  0,  0],
            [ 0,  0,  3,  9,  0],
            [ 0,  0,  0,  4, 10],
            [ 0,  0,  0,  0,  5]])
    >>> rhs = np.array([1, 2, 3, 4, 5], dtype=np.float32)
    

  • solve as single precision real:

    >>> mtx1 = mtx.astype(np.float32)
    >>> x = dsolve.spsolve(mtx1, rhs, use_umfpack=False)
    >>> print(x)  
    [106.   -21.     5.5   -1.5    1. ]
    >>> print("Error: %s" % (mtx1 * x - rhs))  
    Error:  [0.  0.  0.  0.  0.]
    

  • solve as double precision real:

    >>> mtx2 = mtx.astype(np.float64)
    >>> x = dsolve.spsolve(mtx2, rhs, use_umfpack=True)
    >>> print(x)  
    [106.   -21.     5.5   -1.5    1. ]
    >>> print("Error: %s" % (mtx2 * x - rhs))  
    Error:  [0.  0.  0.  0.  0.]
    

  • solve as single precision complex:

    >>> mtx1 = mtx.astype(np.complex64)
    >>> x = dsolve.spsolve(mtx1, rhs, use_umfpack=False)
    >>> print(x)  
    [106. +0.j  -21. +0.j    5.5+0.j   -1.5+0.j    1. +0.j]
    >>> print("Error: %s" % (mtx1 * x - rhs))  
    Error:  [0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j]
    

  • solve as double precision complex:

    >>> mtx2 = mtx.astype(np.complex128)
    >>> x = dsolve.spsolve(mtx2, rhs, use_umfpack=True)
    >>> print(x)
    [106. +0.j  -21. +0.j    5.5+0.j   -1.5+0.j    1. +0.j]
    >>> print("Error: %s" % (mtx2 * x - rhs))   
    Error:  [0.+0.j  0.+0.j  0.+0.j  0.+0.j  0.+0.j]
    

"""
Solve a linear system
=======================

Construct a 1000x1000 lil_matrix and add some values to it, convert it
to CSR format and solve A x = b for x:and solve a linear system with a
direct solver.
"""
import numpy as np
import scipy.sparse as sps
from matplotlib import pyplot as plt
from scipy.sparse.linalg.dsolve import linsolve

rand = np.random.rand

mtx = sps.lil_matrix((1000, 1000), dtype=np.float64)
mtx[0, :100] = rand(100)
mtx[1, 100:200] = mtx[0, :100]
mtx.setdiag(rand(1000))

plt.clf()
plt.spy(mtx, marker='.', markersize=2)
plt.show()

mtx = mtx.tocsr()
rhs = rand(1000)

x = linsolve.spsolve(mtx, rhs)

print('rezidual: %r' % np.linalg.norm(mtx * x - rhs))

• examples/direct_solve.py

2.5.3.2. Iterative Solvers

• the isolve module contains the following solvers:

  • bicg (BIConjugate Gradient)
  • bicgstab (BIConjugate Gradient STABilized)
  • cg (Conjugate Gradient) - symmetric positive definite matrices only
  • cgs (Conjugate Gradient Squared)
  • gmres (Generalized Minimal RESidual)
  • minres (MINimum RESidual)
  • qmr (Quasi-Minimal Residual)

Common Parameters

• mandatory:

  A{sparse matrix, dense matrix, LinearOperator}

  The N-by-N matrix of the linear system.

  b{array, matrix}

  Right hand side of the linear system. Has shape (N,) or (N,1).

• optional:

  x0{array, matrix}

  Starting guess for the solution.

  tolfloat

  Relative tolerance to achieve before terminating.

  maxiterinteger

  Maximum number of iterations. Iteration will stop after maxiter steps even if the specified tolerance has not been achieved.

  M{sparse matrix, dense matrix, LinearOperator}

  Preconditioner for A. The preconditioner should approximate the inverse of A. Effective preconditioning dramatically improves the rate of convergence, which implies that fewer iterations are needed to reach a given error tolerance.

  callbackfunction

  User-supplied function to call after each iteration. It is called as callback(xk), where xk is the current solution vector.

LinearOperator Class

from scipy.sparse.linalg.interface import LinearOperator

• common interface for performing matrix vector products
• useful abstraction that enables using dense and sparse matrices within the solvers, as well as matrix-free solutions
• has shape and matvec() (+ some optional parameters)
• example:

>>> import numpy as np
>>> from scipy.sparse.linalg import LinearOperator
>>> def mv(v):
...     return np.array([2*v[0], 3*v[1]])
...
>>> A = LinearOperator((2, 2), matvec=mv)
>>> A
<2x2 _CustomLinearOperator with dtype=float64>
>>> A.matvec(np.ones(2))
array([2.,  3.])
>>> A * np.ones(2)
array([2.,  3.])

A Few Notes on Preconditioning

• problem specific
• often hard to develop

• if not sure, try ILU

  • available in dsolve as spilu()

2.5.3.3. Eigenvalue Problem Solvers

The eigen module

• arpack * a collection of Fortran77 subroutines designed to solve large scale eigenvalue problems

• lobpcg (Locally Optimal Block Preconditioned Conjugate Gradient Method) * works very well in combination with PyAMG * example by Nathan Bell:

  """
  Compute eigenvectors and eigenvalues using a preconditioned eigensolver
  ========================================================================
  
  In this example Smoothed Aggregation (SA) is used to precondition
  the LOBPCG eigensolver on a two-dimensional Poisson problem with
  Dirichlet boundary conditions.
  """
  
  import scipy
  from scipy.sparse.linalg import lobpcg
  import matplotlib.pyplot as plt
  
  from pyamg import smoothed_aggregation_solver
  from pyamg.gallery import poisson
  
  N = 100
  K = 9
  A = poisson((N,N), format='csr')
  
  # create the AMG hierarchy
  ml = smoothed_aggregation_solver(A)
  
  # initial approximation to the K eigenvectors
  X = scipy.rand(A.shape[0], K) 
  
  # preconditioner based on ml
  M = ml.aspreconditioner()
  
  # compute eigenvalues and eigenvectors with LOBPCG
  W,V = lobpcg(A, X, M=M, tol=1e-8, largest=False)
  
  
  #plot the eigenvectors
  plt.figure(figsize=(9,9))
  
  for i in range(K):
      plt.subplot(3, 3, i+1)
      plt.title('Eigenvector %d' % i)
      plt.pcolor(V[:,i].reshape(N,N))
      plt.axis('equal')
      plt.axis('off')
  plt.show()    
  

  • examples/pyamg_with_lobpcg.py

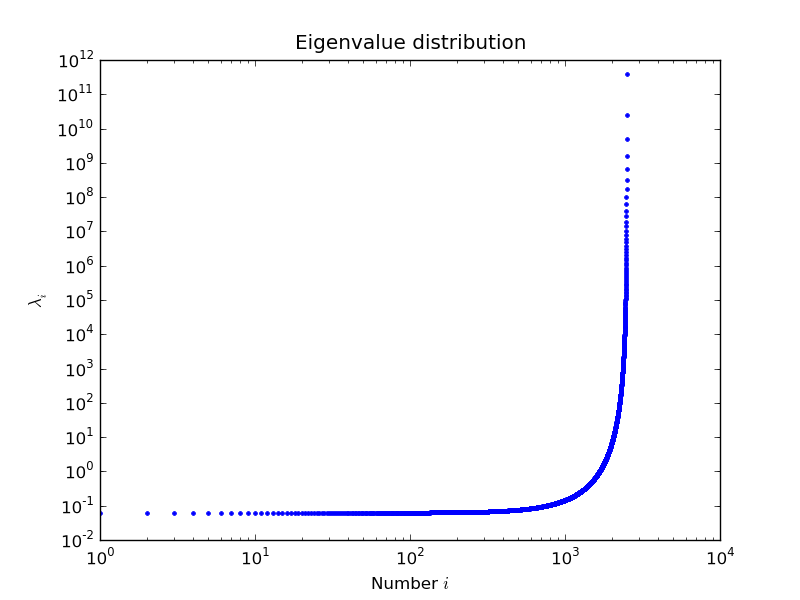
• example by Nils Wagner:

  • examples/lobpcg_sakurai.py

• output:

  $ python examples/lobpcg_sakurai.py
  Results by LOBPCG for n=2500
  
  [ 0.06250083  0.06250028  0.06250007]
  
  Exact eigenvalues
  
  [ 0.06250005  0.0625002   0.06250044]
  
  Elapsed time 7.01